We give a solution to some point:
\begin{align*}
I&=\int_{0}^{1}\left ( \left \lfloor \frac{2}{x} \right \rfloor-2\left \lfloor \frac{1}{x} \right \rfloor \right )dx\\
&\mathop{=\!=\!=\!=\!=\!=\!=}\limits^{\begin{subarray}{c}
{t\,=\,\frac{1}{x}} \\
{dx\,=\,-\frac{1}{t^2}\,dt}
\end{subarray}}\,\int_{1}^{+\infty}\frac{1}{t^2}\bigl({\lfloor{2t}\rfloor-2\lfloor{t}\rfloor }\bigr)\,dt\\
&=\sum_{n=1}^{\infty }\int_{n+\frac{1}{2}}^{n+1}{\frac{1}{t^2}\,dt}\\
&=\sum_{n=1}^{\infty }\frac {1}{(n+1)(2n+1)}\\
&=2\log{2}-1\,.
\end{align*} So \(e^{I+1}=e^{\log4-1+1}=4\) and the geometric series must be converges to \(4\), i.e. \(a<b\) and \[\sum_{n=0}^{\infty }\left ( \frac{a}{b} \right )^n=\frac{b}{b-a}=4\,.\] So we have that \(b=\frac{4}{3}\,a\,.\)
Remains the evaluation of the number \(S=a+\frac{4}{3}a=\frac{7}{3}a\) with the assumption that \({\rm{gcd}}\bigl(a,\tfrac{4}{3}a\bigr)=1\,.\)
\(\bullet\) In the graph below appears that the integral \(\int_{1}^{+\infty}\frac{1}{t^2}\bigl({\lfloor{2t}\rfloor-2\lfloor{t}\rfloor }\bigr)\,dt\) is equal to the infinite sum of the integrals \(\int_{n+\frac{1}{2}}^{n+1}{\frac{1}{t^2}\,dt}\,,\; n\in\mathbb{N}\,.\)
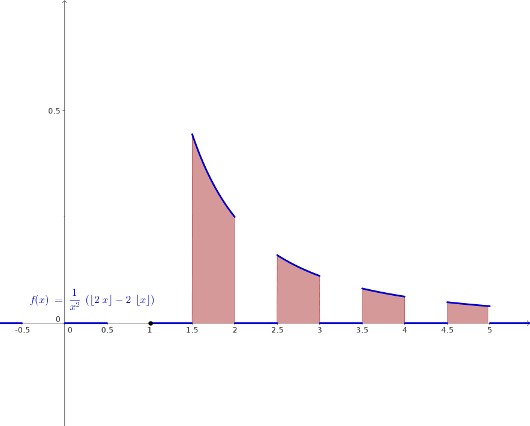
- floorsfunction.png (9.58 KiB) Viewed 2307 times
[/centre]