$\Sigma_{+}=\big\{(x,y,z)\in{\mathbb{R}}^3\;|\; 0\leqslant z\leqslant\sqrt{4-x^2-y^2}\big\}$ is the upper half of the ball with center the origin and radius $2$ and \[\Sigma_1=\Big\{(x,y,z)\in{\mathbb{R}}^3\;\big|\;x^2+y^2\leqslant 2\,,\; \sqrt{x^2+y^2}\leqslant z\leqslant\sqrt{4-x^2-y^2}\;\Big\}\] is the solid which bounded below by the (half) cone $\big\{(x,y,z)\in{\mathbb{R}}^3\;|\; z=\sqrt{x^2+y^2}\big\}$ and above by the sphere $\big\{(x,y,z)\in{\mathbb{R}}^3\;|\; x^2+y^2+z^2=4\big\}$. The intersection of this cone and the sphere is the circle $\big\{\big(x,y,\sqrt{2}\,\big)\in{\mathbb{R}}^3\;|\; x^2+y^2=2\big\}$.
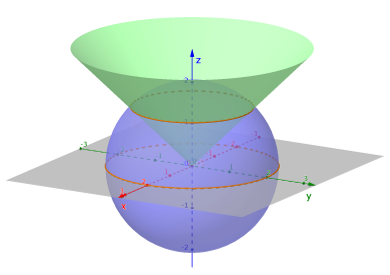
- vol_bwn_sphere-cone.png (34.16 KiB) Viewed 2523 times
[/centre]
The volume in question is $V=V(\Sigma_{+})-V(\Sigma_1)$. It's well known that $V(\Sigma_{+})=\frac{4}{6}\,2^3\pi=\frac{16\pi}{3}$. If $D_1=\big\{(x,y)\in{\mathbb{R}}^2\;|\; x^2+y^2\leqslant 2\big\}$, then the volume of $\Sigma_1$ is \begin{align*}
V(\Sigma_1)&=\displaystyle\mathop{\iiint}\limits_{\Sigma_1}{\rm d}S\\
&=\mathop{\iint}\limits_{D_1}{\sqrt{4-x^2-y^2}-\sqrt{x^2+y^2}}\;{\rm d}(x,y)\\\ &=\int_{-\sqrt{2}}^{\sqrt{2}}\int_{-\sqrt{2-x^2}}^{\sqrt{2-x^2}}{\sqrt{4-x^2-y^2}-\sqrt{x^2+y^2}}\;{\rm d}y\,{\rm d}x
\end{align*} and changing to polar coordinates, we get \begin{align*}
V(\Sigma_1)&=\int_{0}^{\sqrt{2}}\int_{0}^{2\pi}\big(\sqrt{4-\rho^2}-\rho\big)\,\rho\,{\rm d}\varphi\,{\rm d}\rho\\
&=2\pi\int_{0}^{\sqrt{2}}\rho\sqrt{4-\rho^2}-\rho^2\,{\rm d}\rho\\
&=2\pi\int_{0}^{\sqrt{2}}\rho\sqrt{4-\rho^2}\,{\rm d}\rho-2\pi\int_{0}^{\sqrt{2}}\rho^2\,{\rm d}\rho\\
&=\frac{8\pi}{3}\,\big(2-\sqrt{2}\,\big)\,. \end{align*} Thus $$V=V(\Sigma_{+})-V(\Sigma_1)=\displaystyle\frac{16\pi}{3}-\frac{8\pi}{3}\,\big(2-\sqrt{2}\,\big)=\frac{8\pi\sqrt{2}}{3}\,.$$